04/07/2015 A Grécia já encheu o saco O País de Platão e outros ilustres já encheu o saco, o plebiscito de amanhã não tem nenhum sentido, a proposta dos credores venceu na semana passada, sim ou não de que? . O povo grego não tem consciência que a opção técnica virou política. O que dizer do primeiro ministro ter declarado candidamente que “ com o sim ou o não” vai fazer o acôrdo. O plano dos credores para continuar emprestando para os descendentes de Platão, foi elaborado por renomados economistas, só de cálculo exponencial tem um petroleiro cheio. A pergunta é sempre a mesma, como o povo , ora o povo, conseguiria entender tal peça financeira ?. Não entende, só deram a opção do sim ou não,o plano é grego até para eles, nem os imortais do Olimpo entenderiam, quanto mais os mortais não economistas. A verdade do colapso grego é muito semelhante ao brasileiro, gastou mais do que tinha, é a velha teoria que os calouros de economia aprendem cedo, se sair mais do entra, “nóis quebra”. Torraram euros em benefícios sociais que não podiam bancar, será que o Lula, Dilma e equipe deram uma passadinha por là ?. Pelo menos com a Grécia, a Alemanha fiadora e principal interessada em manter a união européia, deu-se mal, da tentativa hegemônica de unificar todos os países do continente sob sua batuta, só os ingleses perceberam a “jogada” e ficaram fora, sorte deles. Caso a Grécia de o calote duas coisas podem acontecer, o euro continua como se nada tivesse acontecido, e isso depende do povo alemão continuar bancando as economias falidas de outros países, , ou, o euro bate as botas e mais uma vez os Fritz ficarão frustados.
Agora leia como parte da matéria acima pode ser lida, imaginem o que tem no meio do tal acôrdo, lembram da Zélia tentando explicar o plano Collor ?. melhor ficar no sim ou não. As funções exponenciais são aquelas que crescem ou decrescem muito rapidamente. Elas desempenham papéis fundamentais na Matemática e nas ciências envolvidas com ela, como: Física, Química, Engenharia, Astronomia, Economia, Biologia, Psicologia e outras. A função exponencial é a definida como sendo a inversa da função logarítmica natural, isto é:
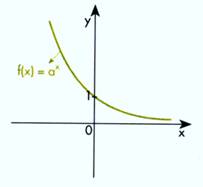
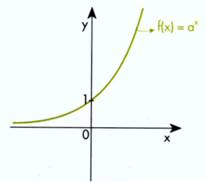
GRÁFICOS DA FUNÇÃO EXPONENCIAL
PROPRIEDADES DA FUNÇÃO EXPONENCIALSe a, x e y são dois números reais quaisquer e k é um número racional, então:
Estas relações também são válidas para exponenciais de base e (e = número de Euller = 2,718…)
A CONSTANTE DE EULERExiste uma importantíssima constante matemática definida por e = exp(1) O número e é um número irracional e positivo e em função da definição da função exponencial, temos que: Ln(e) = 1 Este número é denotado por e em homenagem ao matemático suíço Leonhard Euler (1707-1783), um dos primeiros a estudar as propriedades desse número. O valor deste número expresso com 40 dígitos decimais, é: e = 2,718281828459045235360287471352662497757 Se x é um número real, a função exponencial exp(.) pode ser escrita como a potência de base e com expoente x, isto é: ex = exp(x) CONCLUSÃOPodemos dizer que as funções são utilizadas no nosso dia a dia. Em cálculos rotineiros como em juros, produtividade de uma empresa… A função pode ser expressa graficamente, o que facilita a visualização do cálculo. REFÊNCIAS BIBLIOGRÁFICAS
Hariki, Seiji – Matemática aplicada:administração, economia, contabilidade / São Paulo: Saraiva, 2005. Edson Navarro - Economista |